To find the value of the sine of 45 we use a right isosceles triangle which has the. The sides of a right triangle are commonly referred to with the variables a b and c where c is the hypotenuse and a and b are the lengths of the shorter sides.

Find The Side Length Of A Right Triangle Geometry Lessons Math Memes Right Triangle
If a b and c are the lengths of the sides opposite the angles A B and C in a triangle then.

Sin of a right triangle. The sine of the angle the length of the opposite side the length of the hypotenuse. If we have a right triangle we do not need to use the Law of Sines we should use the basic trigonometry functions we have always used. A trigonometric ratio is a ratio between two sides of a right triangle.
Sin A a c. Lets try a few examples. The key to using the Law of Sines is we must know the value of one angle and the side opposite that angle we must know angle A and side a angle B and side b or angle C and side c.
That means that a right triangle. We can use the Pythagorean theorem and properties of sines cosines and tangents to solve the triangle that is to find unknown parts in terms of known parts. A b c.
In the right-angled triangle ABC the sine of one of the acute angles is 817 what is the value of the sine of the other acute angle. Sine is usually shortened to sin but is pronounced sine. Cos A bc cos B ac.
In this tutorial youll see how to find the sine of a particular angle in a right triangle. Plot of the six trigonometric functions the unit circle and a line for the angle 07 radians. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works.
Tan A ab tan B ba. The points labelled 1 Sec Csc represent the length of the line segment from the origin to that point. Cos A b c.
Sin a tan btan barB sin a tan btan 90circ - B Spherical triangle can have one or two or three 90 interior angle. A right triangle is a triangle with 90 degrees as one of its angles. As the numbers are known on the opposite and the hypotenuse then we look for the ratio which uses both these sides SOH CAH TOA.
B c - a for hypotenuse c missing the formula is. For right angled triangles the ratio between any two sides is always the same and are given as the trigonometry ratios cos sin and tan. In this right triangle the hypotenuse is obviously either 17 or some multiple and one side is 8 or the same multiple of 8.
A2 b2 c2. Since the three angles of a triangle add to and the right angle is frac2 the remaining two angles must also add up to frac2. Sines for common special angles.
If leg b is unknown then. Trigonometry can also help find some missing triangular information eg the sine rule. C a b Given angle and hypotenuse.
The interrelationship between the sines and cosines of frac6 and frac3 also holds for the two acute angles in any right triangle since in every case the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Triangles with more than one 90 angle are oblique. The sine of an angle in a right triangle is equal to the opposite side divided by the hypotenuse.
Sin A ac sin B bc. Their angles are also typically referred to using the capitalized letter corresponding to the side length. The Sine Rule The Law of Sines sine rule is an important rule relating the sides and angles of any triangle it doesnt have to be right-angled.
Sine is a trigonometric ratio comparing two sides of a right triangle. That ratio is the sine ratio. First label the sides.
The values of the sines of the most important angles can be found using the proportions of the special triangles. I will assume the sides are 17 and 8 because the argument will be the same. The Law of Sines applies to any triangle even right triangles.
A c sin or a c cos b c sin or b c cos Given angle and one leg. Apply the law of sines or trigonometry to find the right triangle side lengths. Trigonometry is the study of the relationships within a triangle.
Spherical triangle is said to be right if only one of its included angle is equal to 90. The three main trig ratios are sine cosine and tangent. In a right triangle the side that is opposite of the 90 angle is the longest side of the triangle and is called the hypotenuse.
In this right triangle. In any right angled triangle for any angle. Tan A a b.
The sine ratio is just one of these ratios. Using this we have the relations y in the triangle above. This function can be used to determine the length of a side of a triangle when given at least one side of the triangle and one of the acute angles.
Angle A for side a angle B for side b and angle C for a right triangle.

Right Triangles And Trigonometry Graphic Organizer Reference Sheets Freebie Trigonometry Math Methods Gcse Math

Diagram Of Sine Ratios Gre Math Sat Math Math Geometry

Right Triangle Trigonometry Finding Angles Inverse Functions Youtube Trigonometry Math Signs Education Quotes

Special Right Triangles Math Examples Trigonometry Worksheets Trigonometry

Soh Cah Toa Studying Math Math Methods Gcse Math

Right Triangle Trigonometry Worksheet Answers Trigonometry Worksheets Trigonometry Mathematics Education

Sine Cosine Tangent Trigonometry Studying Math Triangle Math

Law Of Sines Law Of Sines Sines Law

Pin On Teaching Math Trigonometry

The Law Of Sines Provides A Formula That Relates The Sides With The Angles Of A Triangle This Formula Allows You To R Law Of Sines Math Methods Education Math
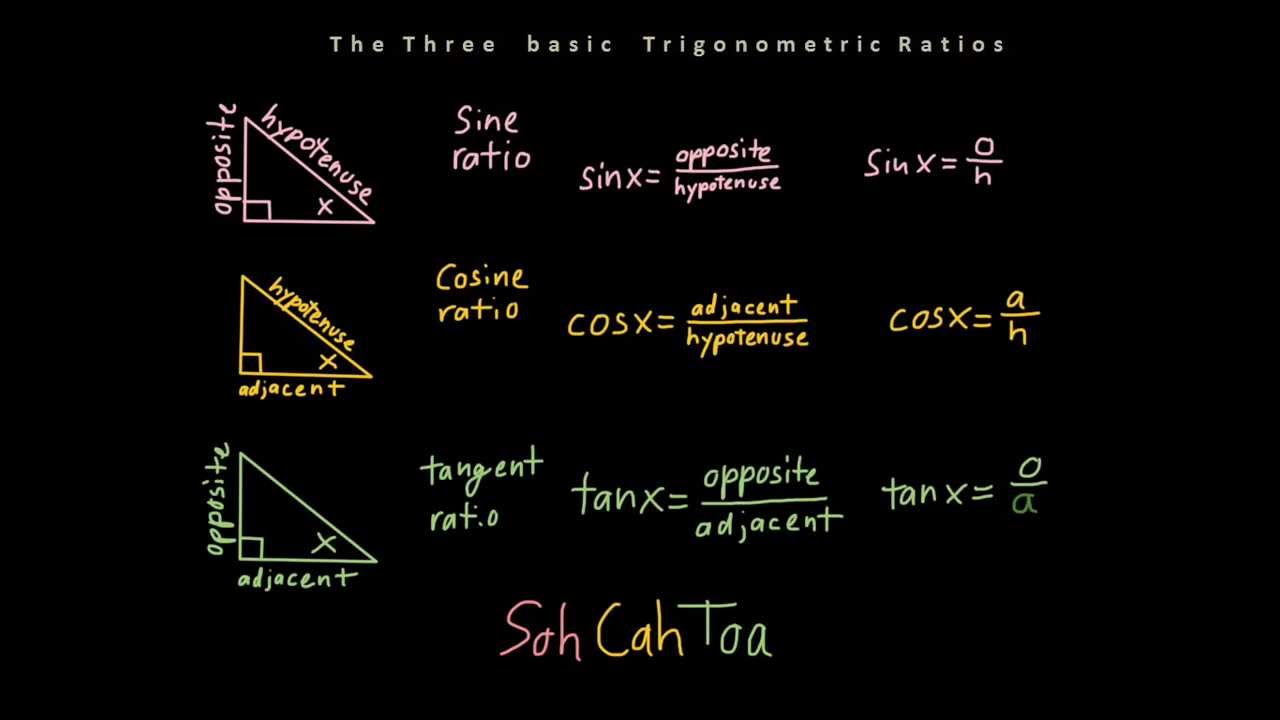
Pin On Studypoint Sat Act Study Tips

Sine Cosine And Tangent Ratio Formulas Trigonometry Math Memes Math Formulas

Formulas For Right Triangles High School Math Geometry High School Education Math

A Right Triangle Def Is Shown To The Left Of The Text That Describes The Three Trigonometric Ratios The Sine Of Angle F Is Op Right Triangle Opposites Tangent





